Unless you’re hard of hearing, you have heard harmonics before, if not of harmonics. They are found in many naturally occurring periodic phenomena like sounds coming out of vocal cords or a musical instrument. In this post, I present a simple argument/animation for why harmonics exist.

For phenomena that repeat with some fundamental period $T$ or frequency $f=\frac{1}{T}$, harmonics are integer multiples of the fundamental frequency ($nf = n/T$). When you listen to a guitar playing a tone or a flute playing the same tone, say 440Hz, you hear the fundamental frequency as well as the harmonics (880Hz, 1320Hz, etc.) of the vibrations. Here is a microphone recording of my Ukulele’s G string vibration. The plot represents how the air pressure fluctuates around the microphone; larger the string vibration amplitude, larger the amplitude on the plot.

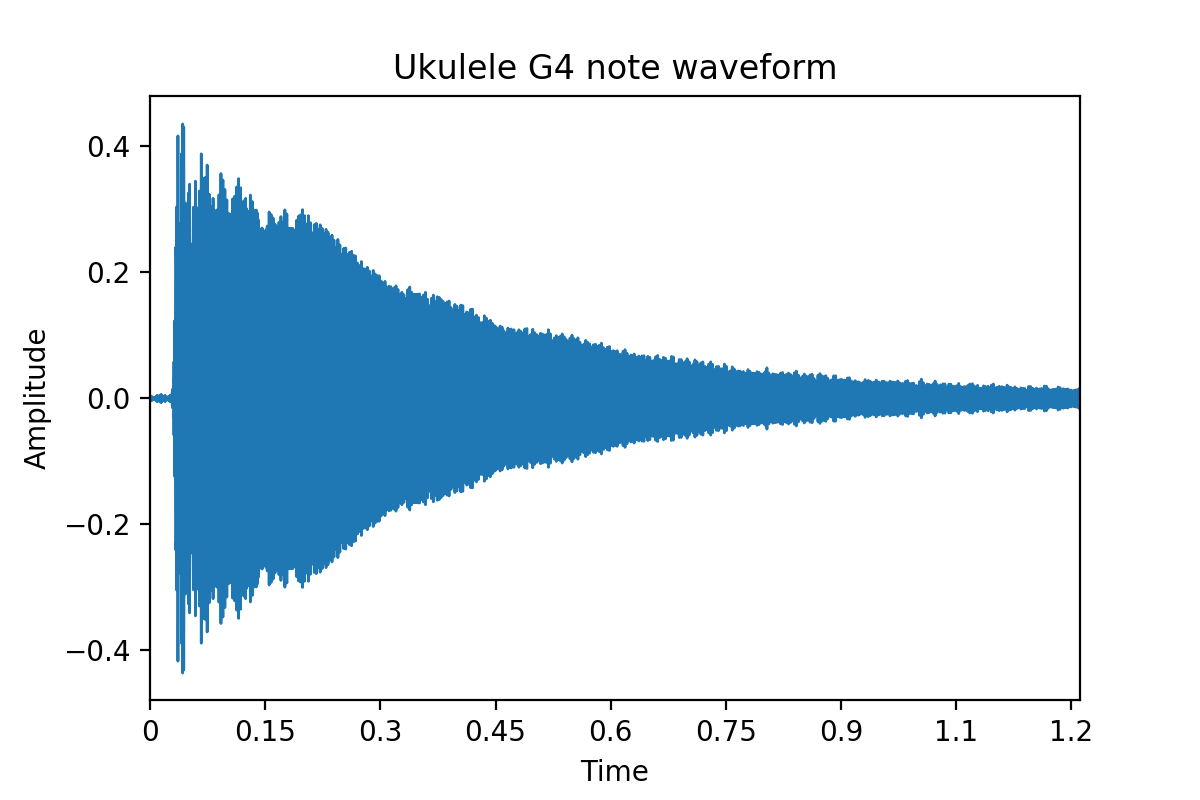
The waveform has a strong attack and a slow decay.

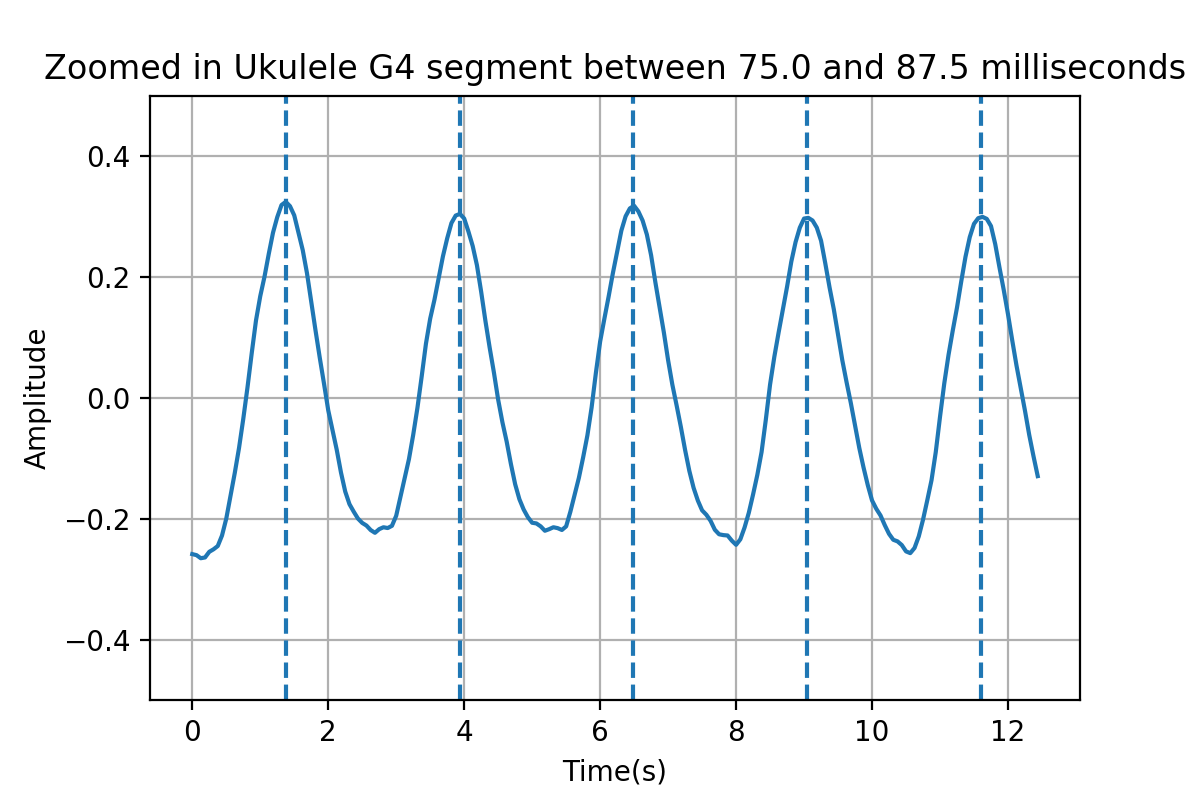
The Ukulele plays a G4 note which is 391Hz. If we zoomed in to a small segment, we can see that the waveform is repeating every 1/391 seconds. The lines were drawn by finding the first peak and adding 1/391 to get the next peak. Notice how the waveform shape repeats quite perfectly.

Does it contain harmonics? Yes, if we plotted the Fourier transform, you can observe energies at integer multiples of the fundamental frequency. Notice below how the first 10 multiples of the fundamental 391Hz align quite well with the peaks of the magnitude of the fourier transform. The higher frequencies might be attributed to noise.

The relative intensities of the fundamental and harmonics are what tells you the two instruments are different. Different guitar strings or flute holes are tuned to cause the instrument to resonate at different fundamental tones. Now, where do these integer multiple harmonics come from? In high school physics, we learn that this is due to the fact that standing waves form on a guitar string or air inside a flute. The standing waves only form to have energy at the fundamental frequency and its harmonics.

Next, a second context for harmonics. If we asked your computer speaker to generate a pure tone by giving the speaker as input a sine wave of a fixed frequency and then record that audio via a microphone, we again observe harmonics in the microphone recordings. We call these unwanted harmonics, distortion and measure the total harmonic distortion (THD) as the ratio of energy in all of the harmonics to the energy in the fundamental. The distortion could be coming from either the speaker or the microphone.

It turns out that if a system like a loudspeaker is non-linear, it can generate these harmonics given some input. This is by definition, because a sine wave input into a linear time-invariant (LTI) system will only produce sine wave output of the same frequency as the input, with possibly different amplitude and phase. Thus, if there are harmonics, they must have been injected by a non-linearity in the system. What kind of non-linearities would generate harmonics and why integer multiples of the fundamental as opposed to arbitrary frequencies?

Harmonic distortion from speakers and harmonics from musical instruments exist because of the same fundamental idea of how periodic functions behave. We will start by looking at graphs of behaviors of periodic functions and then discuss how they apply to the two contexts above.

Anatomy of a periodic function Link to heading

A function $u(t)$ is periodic if it repeats its values every $T$ period: $u(t+nT)=u(t)$. $u(t)$ is also periodic with periods $2T$, $3T$ etc. but we choose to refer to the fundamental period as $T$. We have complete knowledge of the function or signal $u(t)$ if we know its shape in the period $T$.

Sums of periodic functions Link to heading

If we add two periodic functions $u(t)$ and $v(t)$ with periods $T_1$ and $T_2$, $u(t) + v(t)$, the sum is generally periodic. It is periodic if there are positive integers $a$ and $b$ that satisfy $aT_1 = bT_2 = r = \text{LCM}(T_1, T_2)$. $r$ is a period of resultant sum but it’s not always the fundamental period. For example, $sin(2\pi x)$ and $-sin(2\pi x)$ are both periodic with period 1 but their sum is 0 and had no fundamental period.

One situation where the sum of two periodic functions is not periodic is when $a$ and $b$ don’t exist. For example, if $T_1=1$ and $T_2=\sqrt{2}$.

For engineering purposes, we can say that the sum of periodic functions is periodic.

Decomposing a periodic function Link to heading

Given an arbitrary periodic function $u(t)$ such as the Ukulele plot, can we decompose $u(t)$ into a sum of simple periodic functions?

From the previous section, we know that if we added up periodic functions (call them the basis functions), we would end up having a periodic function. Let’s choose as our building blocks the sine function, $\sin(t)$. It has a period of $2\pi$. Alternatively, $\sin(2\pi t)$ has period 1 because $\sin(2\pi (t+1)) = \sin(2\pi t+ 2\pi) = \sin(2\pi t)$. Generally, $\sin(\frac{2\pi t}{T})$ is periodic with period T. Decompose $u(t)$ as a summation of k sinusoids with periods $T_k$ and phases $\phi_k$:

$u(t) = \sum{c_k sin(2\pi t/ T_k + \phi_k)}$

How do we choose the periods $T_k$ of these basis periodic functions so that their effective period is equal to a given $T$?

The answer is the punchline. First, the period of a basis function cannot be greater than T, otherwise the sum would be periodic with at least period T. The sum’s period is going to only repeat itself after the longest period among its basis functions is complete. Second, the only basis functions that would be periodic with $T$ are those that have period either $T$ or an integer divisor of $T$, $T/k$ called the harmonic. To see this, here is a sine wave with period $1$. On top of it is an animation of sine waves with all the possible periods starting at $1$ and going till the 5th harmonic ($k=5$). Observe which functions are periodic with period T. The sine wave turns red at these points. Feel free to move the animation time slider back and forth and pause around these points.

So this is where harmonics come from. If you have a periodic signal with a fundamental frequency $f_0 = 1/T$, then it can only have contributions from basis functions that have harmonic frequencies $f_1=2/T, f_2=3/T…$.

Such a decomposition of a periodic function is the Fourier series.

Systems and harmonics Link to heading

What about the loudspeaker situation? Why did that produce harmonics when we asked it to play out a pure tone? The imperfections in the sound reproduction/capture process introduced some shape distortion but at least it preserved the pure tone period. For example, it might have clipped if the input signal was too loud leading to a signal that looks like this:

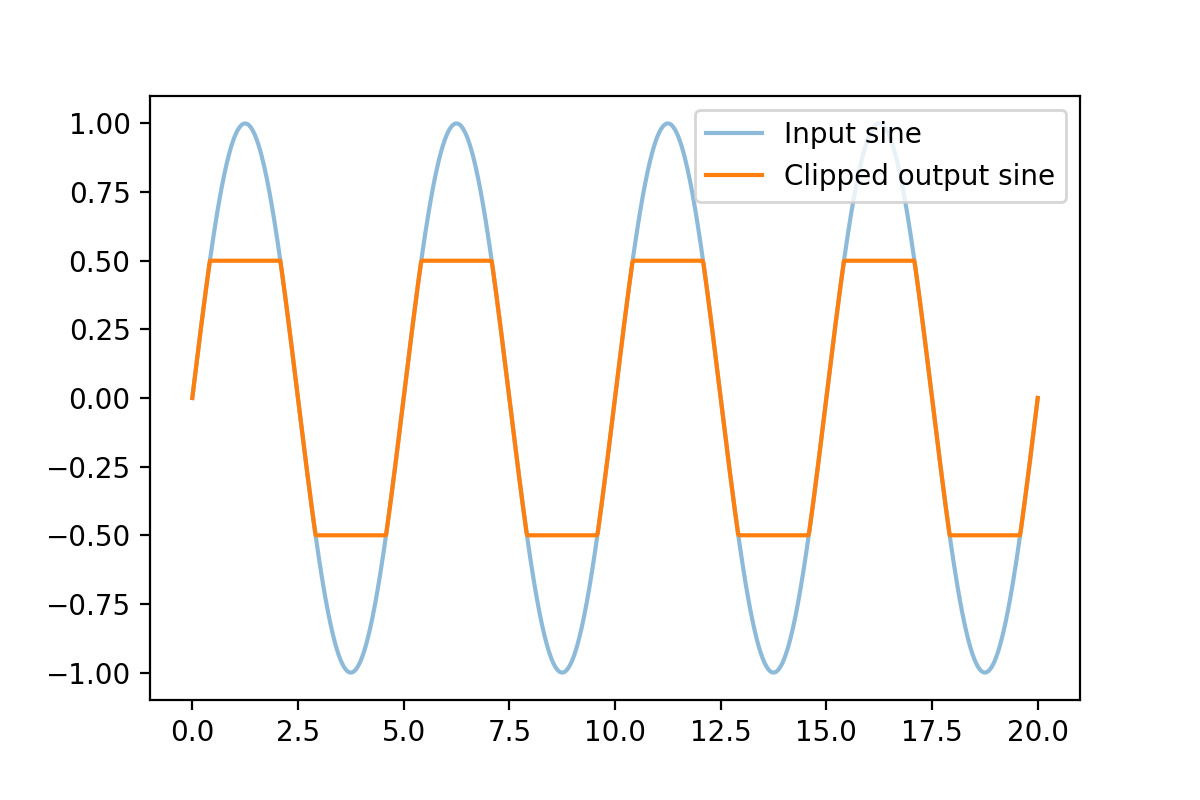
The Fourier transform for this signal looks like this:

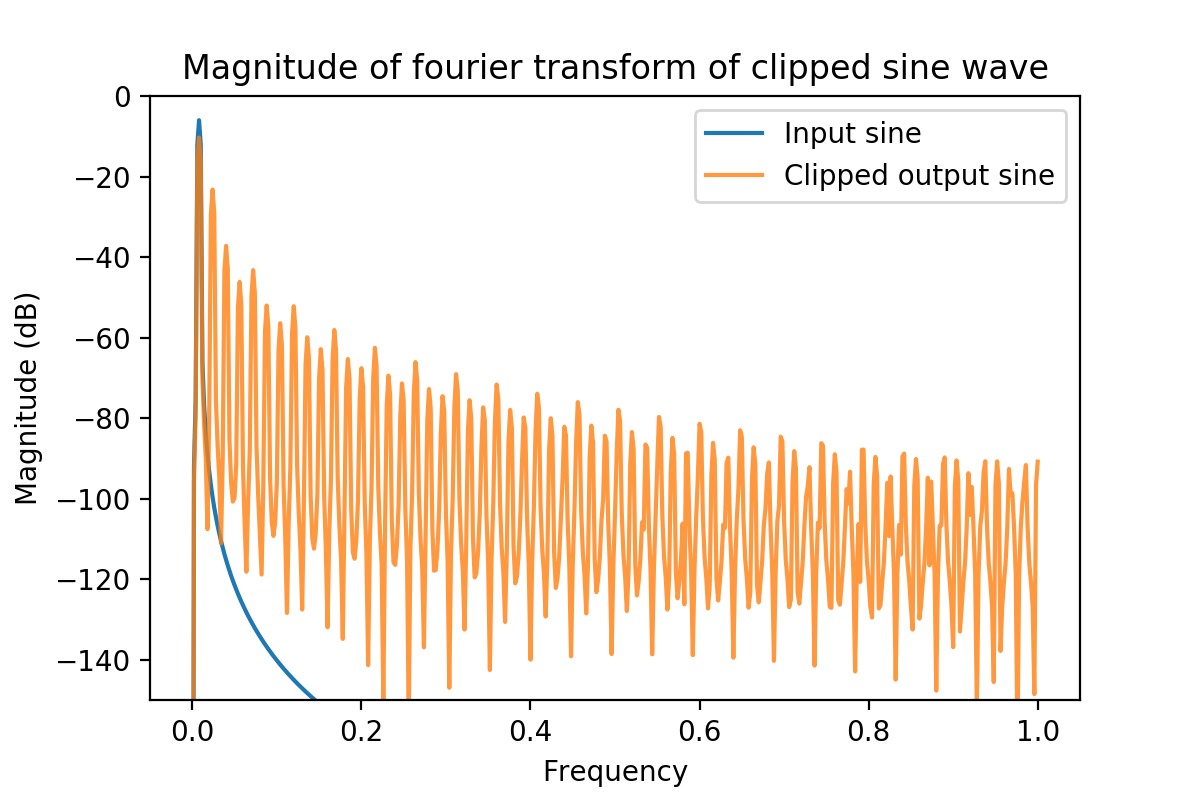
Clearly visible are the harmonics. Because the “non-linearities” preserved the fundamental frequency but changed the waveform shape, energy appears in integer multiples.

Of course, there can also be non-linear systems that will alter the fundamental frequency itself. Interestingly, if $T$ is the period of function $u(t)$ and $H$ is a system/function acting on it, then $H(u(t))$ will also have a period $T$ but the fundamental period could be smaller. A simple non-linear operation that would do that is the square operator:

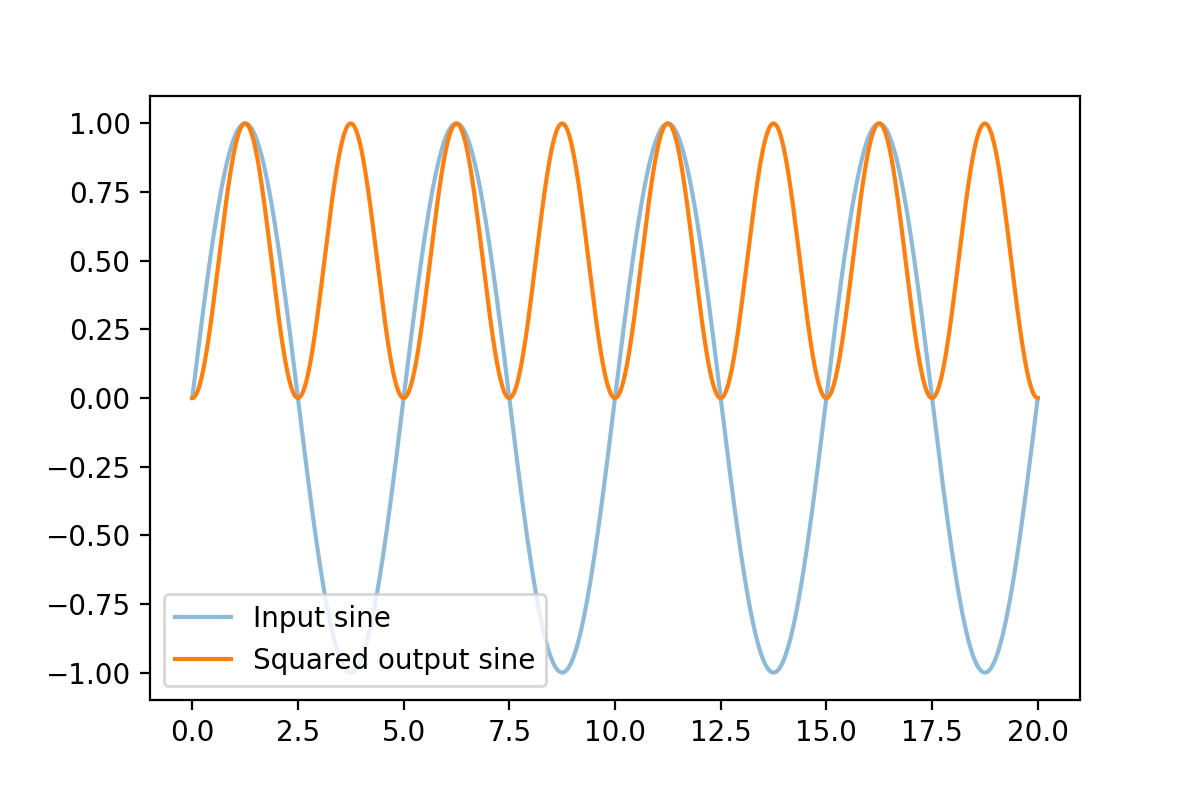
Notice how now the average of the signal is non-zero. This shows up as energy at 0 frequency in the frequency plot below.

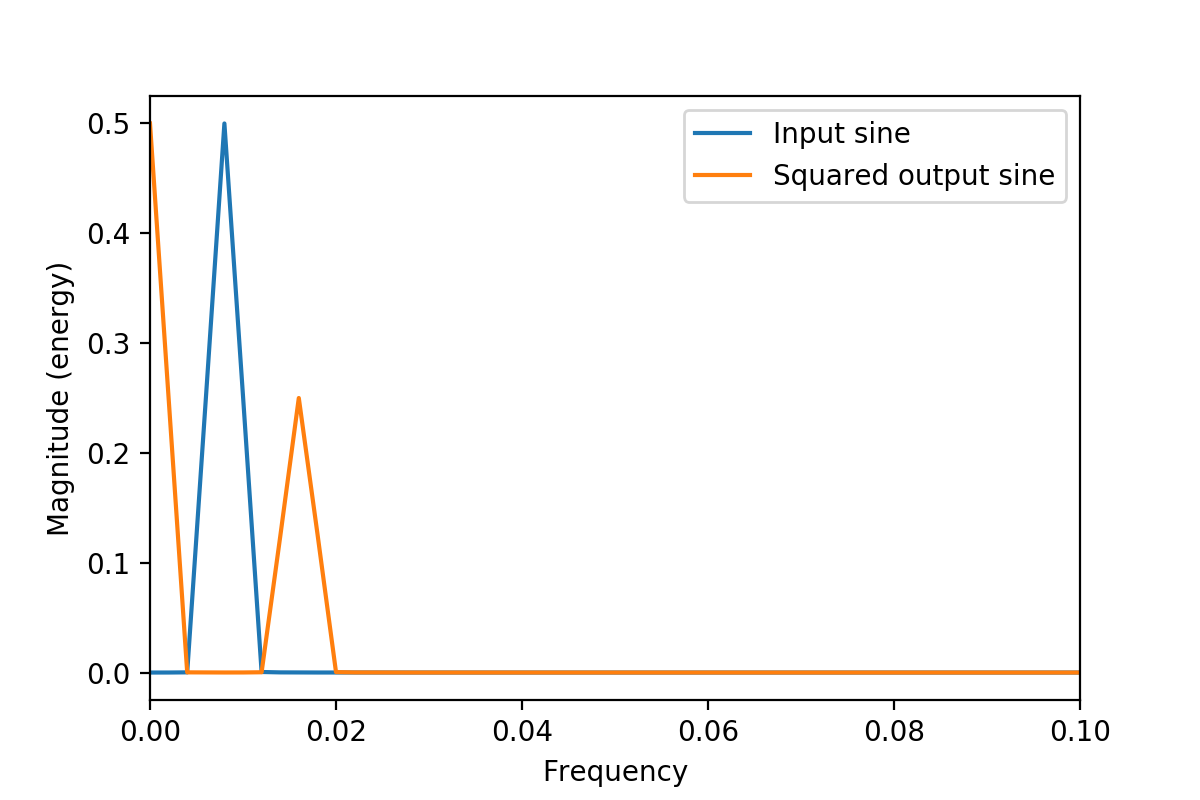
The fundamental frequency is now twice what it was since as you can see from the time domain plot, the wave shape repeats with half the period as before.

Conclusion Link to heading

We looked at how harmonics show up when have periodic phenomena with some fundamental frequency $f_0$. Their existence was explained through a simple argument: only integer multiples of $f_0$ have period corresponding to $1/f_0$. If a complex periodic function is to be broken down into a sum of basis functions, those functions have to obey this constraint of being harmonics so that the resultant summation has the same period as the original signal.